What Is The Nash Equilibrium In This Dorm Room Cleaning Game?

Although not totally right, information technology'south oft written that social interactions are what make humans very different from animals. In fact, Joel Brown, a renowned professor in ecology, one time told me that, as a result, game theory ruled our every 24-hour interval's lives. While naive people play games they are non enlightened of, paranoid people imagine themselves playing a game when they are not. The movie "A Beautiful Heed" displays how the great American mathematician John Nash overcame an sickness which made him belong to the latter sort of people. But that's not what John Nash is famous for. In the middle of the 20th century, his cute mind brought major concepts to the emerging game theory, commencement divers for nil-sum games and so extended to cooperative games by John von Neumann and Oskar Morgenstein. Game theory is present, 50 years afterward, an incredibly dynamic field of inquiry.

I'll present some of the major concepts of game theory through classical examples of games. More avant-garde concepts including extensive grade, Stackelberg games, mechanism blueprint, evolutionary game theory and mean field games are dealt with in my commodity on avant-garde game theory. Nonetheless, I'm not going to detail these concepts a lot in this article. Then I'k counting on you lot to write other more detailed articles on these concepts for more accurate understanding of them.

Separate or Steal

Dissever or Steal is the catastrophe role of a British TV game show. The two contestants are faced with a sure amount of money. Each of them needs to determine whether to split this amount or to steal information technology. The option is fabricated without the contestant'southward cognition. If both steal, then the money is given to no one. If one steals and the other splits, then the coin goes all to the stealer. If both carve up information technology, they each get half of the money. The post-obit video displays an excerpt from the prove.

The contestants are unremarkably called players or agents. Here, each player can choose to dissever or steal. These are his possible deportment. In the game, at that place are two possible deportment for each role player. Since the game involves 2 players and is finite (that is, for each player, the number of possible actions is finite), it tin can exist described with two matrices, called payoff matrices, which displays the gains (or payoffs) of each player. These games with ii players and finite sets of deportment are chosen bimatrix games. Below are displayed the two payoff matrices.

Notice that, for each player, no matter which action the other chooses, one activeness is always better than the other. We say that playing this better activity is a dominant strategy. Information technology's the case of stealing in the Split or Steal game. Equally a result, if there is no cooperation and if each role player is selfish, they volition both play the ascendant strategy. Nevertheless, each actor would prefer that the other plays the dominated strategy. In our example, each histrion is hoping that the other will dissever. Thus, whatever rational player has incentive to human action similar he's going to cooperate to encourage the other to cooperate also, but eventually, if the action tin exist made secretly from the other, he should not cooperate.

Only that's not what happens, is it?

In the Television set show, there is also a matter of ideals linked to honesty, which may lead players to split. Too, winning one-half the total all the same sounds similar winning, maybe fifty-fifty more, for some people, than actually winning the total. These two remarks can exist summed up by saying that the proceeds of the players cannot exist reduced to the financial gain, and it tin can be modeled past taking into account other factors in the actual gains. Some other explanation may prevarication in the fact that players have not made all of our reasoning…

The Prisoner's Dilemma

The Prisoner's Dilemma is the virtually famous instance of Game Theory, stated in 1950. Herminio Lopez gave an illustration in soccer tournaments. Check the bang-up following video by Instant Egghead to sympathise it well.

Basically, 2 suspects who cannot communicate tin can denounce each other. If they do denounce, their penalty is diminished. Just if they are denounced, they go a big penalization. The following table displays the payoffs respective to the case of the video (except that I have replaced 1 month past 1 year for simplicity of notations). Note that I have merged the two payoff matrices into an array. This is the most common representation of 2-player games with finite sets of actions.

Just similar in Dissever or Steal, we tin can observe that betraying is the ascendant strategy, even though it's not the ane the other player hopes will be played. Because betraying is ascendant, the strategy profile where both beguile is a Nash Equilibrium.

What'due south a Nash Equilibrium?

A Nash Equilibrium is a strategy profile such that, for each player, assuming that others will play accordingly to the strategy contour, there is no meliorate strategy than playing according to the strategy profile. Equivalently, no actor has incentive to deviate unilaterally from the strategy profile. Equally a outcome, if players make a bargain to play a Nash Equilibrium, and if, after that, each player plays secretly without advice, then you can be confident that they will all follow the deal. Indeed, each of them, assuming that others follow the deal, has incentive to follow the deal.

And so the strategy profile where all players play dominant strategies is always a Nash Equilibrium, isn't it?

You lot are right! Merely there'southward actually more: If each player has ane strictly dominant strategy (that is, ever strictly meliorate than all other strategies), then the strategy profile where all play their dominant strategies is the only Nash Equilibrium. Indeed, no affair what others do, it is always better to play the strictly ascendant strategy.

Simply do prisoners really play the Nash Equilibrium in real life?

Not always… This commodity indicates that prisoners exercise play it one-half of the time. What's particularly agreeable is to see that students play it much more than often, which sort of indicates that the moral of cooperation is much stronger for prisoners than students! A cistron which may explicate that is the fact that this game is repeated, in the sense that y'all'll still have to face up the other prisoners or students the next days…

So game theory basically sums up to finding dominant strategies?

Well, that'd exist as well easy… Quite oft, there is no dominant strategy. Just similar in the battle of sexes.

Boxing of the Sexes

The battle of the sexes is a classical example of the more general instance of coordination games. Imagine a married couple who needs to determine what to do in the evening. The wife has mentioned the opera, while the husband has suggested the football match. However, their cellphones have run out of bombardment and they cannot communicate. They each accept to decide where to get. Plain each prefers the identify he has proposed, but both prefer being with the other than anything else. Here is the payoff matrix.

I oasis't establish whatsoever good video example of that… If you lot take any thought, please contact me!

As you said, at that place is no dominant strategy here…

Exactly! Notwithstanding, there are two Nash Equilibria here…

They represent to the top left and the bottom right cases, right?

Indeed. If the wife and married man concur to get to the opera, and therefore expect the other to go in that location, and so in that location is no better strategy for them than actually going in that location. Therefore, the strategy profile where they both go to the opera is a Nash Equilibrium. Similarly, the case where they both become to the football match is besides a Nash Equilibrium.

Simply one of them will necessarily exist taken in…

Especially if, with time, the couple's desire to spend the evening together decreases (I hope information technology won't be the example for yous!). Past subtracting i to the gains when they are together, we at present have the following payoff matrices:

The Nash Equilibria would still remain Nash Equilibria, but there will no longer be strict Nash Equilibria. As a matter of fact, knowing that his wife volition go to the opera, even though there is no better strategy for the man than going to the opera, going to the opera is not strictly ameliorate than going to the football game match. In fact, going to the football game match is for him a dominant strategy. Just if both players play their dominant strategy, and so nosotros also accept a Nash Equilibrium. Every case of the table is now a Nash Equilibrium.

Well, that's bad…

That's where comes the concept of correlated equilibrium. For a correlated equilibrium, players take into account an external indicate that hints them at playing a specific strategy. Now, given his signal, each thespian tin can assume which point the other may have with a certain probabilistic distribution simply he does not know the other'due south signal for sure. If, given the probabilistic distribution of signals for the other, each histrion still has incentive to follow the hint of the signal, then the betoken arrangement forms a correlated equilibrium.

Applying this in our example is rather easy: the couple may flip a coin. Head is the opera, tail is the football game match, for case. Every bit a result, in means, if they do that every week, they'll both be happy and equally happy. Here I'm just having an overview of correlated equilibria… Don't hesitate to a write your own commodity on this concept!

Cooperative Games

What all the examples we have seen so far show is that…

People should cooperate instead of being selfish, right?

Indeed. That'southward why game theorists like to think about what could happen if players actually cooperated. The trouble is that, in the games we gave mentioned, by cooperating, they lose something by non deviating from the cooperation. We oft need to compensate them past reallocating the gains of the cooperation. This reallocation, chosen solution concept, tin be crucial and hard to be done. That's where comes cooperative games theory, as opposed to non-cooperative game theory we take studied so far.

The major concept in cooperative games is the Shapley value, introduced by Nobel prize winner Lloyd Shapley. It gives a fair-plenty style to reallocate the gains. Its idea is to allocate to each person the means of what he gives to whatsoever coalition he would enter, with more important weights to larger coalitions. The Shapley value is interesting because it yields several properties (efficiency, symmetry, additivity, zero player). I requite a more than complete definition of the Shapley value in my article on fair sectionalisation.

This sounds great!

Yes! Just the Shapley value also has flaws. Mainly, it is non necessarily a Nash Equilibrium, as it's possible that players nonetheless have incentives to go out of the coalition. Consider Divide or Steal for instance. A cooperation game would atomic number 82 to the both players winning together all of the sum so sharing it deservedly. It's still improve to steal the money…

More than more often than not, it'south also possible that a subset of players would have incentives to become out of the one thousand coalition, that is the coalition with all players. That'south the example in the example of miners. Suppose in that location are iii of them, but at that place only needs to exist two of them going the mine and bringing dorsum all of its gold. If but one goes, he won't exist able to bring back anything. A Shapley value would get all miners going to the mine and splitting the booty in three equal shares. Just two of the miners would accept incentive to go to the mine without the third one, hence sharing the haul in two equal shares. In cooperative game theory, we say that the yard coalition and the solution concept are not stable. Many researches focus on the ready of stable solution concepts for the k coalition is called the core. However, this core is generally hard to study and information technology might be empty. These concepts take other flaws that I mention in my article on fair segmentation.

The concept of the core is shut to another concepts in non-cooperative games: the concept of strong Nash Equilibrium. Recall that a Nash Equilibrium is a strategy contour such that no thespian has incentive to deviate from unilaterally. Now, a potent Nash Equilibrium is a strategy profile such that any subset of players has no incentive to deviate from collectively.

Can y'all requite an case?

Sure! Let's consider again the initial battle of sexes. However, this time, we assume that the husband has taken lessons of musics and he at present enjoys the opera merely as much equally football. We may now accept the following payoff matrices:

In this example, even though it is still a Nash Equilibrium, the strategy contour where both go to the football game match is not a strong Nash Equilibrium. As a matter of fact, if the couple collectively deviates from the bottom right case to the top left case, then they volition both exist at least as happy, and one of them will be strictly happier.

Then strong Nash Equilibrium is a more restrictive concept than the Nash Equilibrium?

Yes. Any strong Nash Equilibrium is a Nash Equilibrium but the changed is not necessarily true.

Cournot Contest

It's time for you to learn about the beginning major application of game theory. Designed past the French mathematician Antoine Augustin Cournot in the middle of the 19th century, the Cournot competition illustrates how competition yields a decrease of prices. More precisely, information technology displays the fallouts of duopoly equally opposed to monopoly. I'm not going to explicate it in details though. You lot are more than welcome to write an article on the topic!

In the Cournot contest, 2 companies produce the same good. They each choose a quantity to produce. This option is their action. Nosotros shall notice that the prepare of deportment hither is infinite. At present, depending on the full produced quantity and the demand curve, a price is given. Each visitor'south profit is the product of his production past the difference between the toll and the marginal cost (the toll of producing i unit of production). The objective of each company is the maximization of its profits.

In the figure, visitor 1 chooses the quantity of Cie 1, while company 2 chooses the quantity of Cie 2, as they each attempt to maximize their profits, which is the area of the dark-green and blue rectangles.

It's of import to notice that each company's best choice of the quantity to produce depend on the other company's choice. If the other company produces a lot, so the prices will be low, and producing a lot can atomic number 82 to negative profits. But if the other visitor does non produce a lot, there is an incentive to produce a lot, knowing that the prices will remain high plenty. Nosotros telephone call the best choice of a visitor given the other company's choice a best response to the other company's strategy. Notice that a Nash Equilibrium can be defined as a strategy profile such that any player's strategy is a best response to the other company's strategies.

The problem can be solved in simple models where the demand is linear and the marginal cost is constant. It tin be shown that, at the Nash Equilibrium, the total production is higher than if a single company was producing to maximize its profits. Equally a result, the prices are lower. Although simple, this illustration has been the footing of many reasonings of economists.

Princess and Monster

I am now going to present very briefly a more complicated game called Princess and Monster, which volition help u.s.a. introduce some other major concept in game theory. This game is a specific example of the more full general case of pursuit-evasion games. Let's consider the classical game of Nintendo, where the Monster Bowser is pursuing the Princess Peach, who must be saved by the Italian plomber Mario.

At present, Princess and Monster consists in Bowser chasing Peach in a given divisional room. Simply the fox is that the light is off. Although they both know what the room is like, they take no idea where the other is. Now, Bowser has to find Peach as soon as possible, considering, for instance, he knows that Mario can get in at whatever fourth dimension. In this prepare, if Peach'southward run in the room is known by Bowser, so Bowser'southward strategy tin can be chosen accordingly. Similarly, if Bowser's run is deterministic, Peach can run accordingly. Just if Peach chooses her run randomly, Bowser will have to adapt his run to minimize the expected time of capture, which will requite him more trouble. The same reasoning can be done for Peach.

Why are you lot bold that each player knows the other'south strategy?

First, this is a particularly common supposition, especially if you consider that players play repeatedly. Eventually, they know what strategy the other is playing. But mainly, the concepts of best response and Nash Equilibria involve knowing the other player's strategy.

Introduced by Rufus Isaacs in 1965, the Princess and Monster problem had been open problem for more than a decade, until it was solved by Shmuel Gal in the late 1970s. As expected, the Nash Equilibrium consists in players choosing their run randomly. Such strategies are called mixed strategies, by opposition to pure strategies, for which actions are called deterministically. The mixed strategy is therefore a mixture of pure strategy with different probabilities of playing each of the pure strategy.

What's the Nash Equilibrium of Princess and Monster?

Plainly, it depends on the characteristics of the room and of the players. Just, according to Wikipedia, Nash Equilibria all have the following characteristic: Peach'south strategy at equilibrium is to run to some randomly chosen location in the room and stay for a while. And repeat this procedure indefinitely. I'm not very familiar with pursuit-evasion and search games. Your help, by writing an article for instance, is more than than welcome!

Rock Paper Scissors

Stone Paper Scissors is a very basic popular 2-player game. Each histrion chooses Stone, Paper or Scissors, knowing that Paper covers Stone, Pair of scissors cuts Paper and Stone crushes Pair of scissors. This gives us the following payoff matrices:

Let's search for Nash Equilibria…

None of the cases is a Nash Equilibrium?

Exactly. In whatsoever instance, one of the players is not winning. Nonetheless, for any case, players tin deviate and get a winning case.

So is at that place no Nash Equilibrium?

Really there is, co-ordinate to Nash'due south theorem. This is one of the shortest major theorem I know: Any finite game has a mixed-strategy Nash Equilibrium. The proof involves a fixed indicate theorem, only it'southward way too complicated for me to dwell on hither. Permit's simply trust John Nash.

So I guess that for Stone Paper Scissors we should search for Nash Equilibrium with mixed strategies…

Exactly. And nosotros'd find that the equilibrium is for both players to play uniformly randomly one of the 3 pure strategies. If the other player does that, then doing that too, merely like playing whatsoever strategy, would yield an naught expected payoff. Thus, in that location is no amend response than the mixed strategy we take described, and it is therefore a all-time response to itself, which proves that it'south a Nash Equilibrium.

In fact, two other properties of Stone Newspaper Pair of scissors would have led united states of america to final to the being of a mixed strategy which yields a goose egg expected payoff for both players. The first property to detect is that information technology is a nada-sum game, that is, whatever player 1 wins, thespian 2 loses information technology. Equivalently, and information technology'southward easy to see on the tabular array, their gains always sum up to 0. The minimax theorem by John von Neumann in 1928, tells us that, for any nothing-sum game, the best ane role player can get by announcing his strategy first is equal to the best he can become by reacting to a smart opponent's strategy. As a consequence, nil-sum games all have Nash Equilibria, which all yield the same expected gains for player 1, as well as the same expected gains for role player 2. There is much more to say, and you are welcome to do and then!

What'south the second property?

The second property is the symmetry: The rules are the same for both players. This can be observed in the payment matrices. The transpose of histrion two's payoff matrix is equal to player ane's payoff matrix. As a event, the payoffs at a Nash Equilibrium of both players must be the same. Since it'south a cypher-sum game, their payoffs must also add up to 0. Thus, their payoffs are necessarily 0.

For the fun of it, I'll mention that one flaw of this game is the relatively frequent occurrence of equalities when playing Nash Equilibria. That's one affair that Rock Paper Scissors Cadger Spock corrects:

The Nash Equilibrium is still playing 1 of the action uniformly randomly, because of the symmetry between the different deportment, which tin be noticed in the following figure:

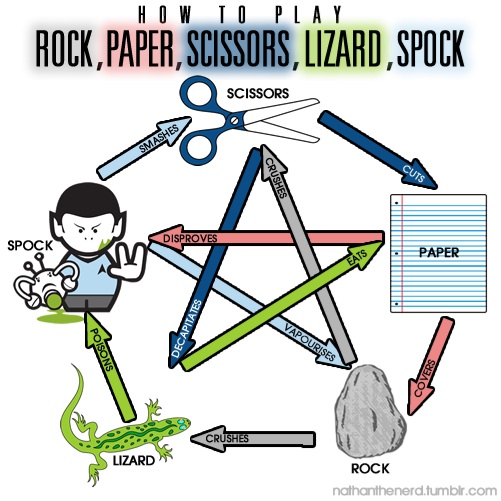
Rock Paper Scissors is very interesting for the report of Evolutionary Stable Strategies. Find out more in this article.

Allow's sum up

Game theory is a very big field and we have barely scratched its surface. I hope this read has interested you, and if information technology has, I tin can only encourage yous to read more virtually it. For a start, please read my overview of avant-garde game theory. Or check the applications of game theory to predictions in geopolitics by the heed-blowing Bruce Bueno de Mesquita.

Source: https://www.science4all.org/article/game-theory/

Posted by: gonzalezplarecturs.blogspot.com

Share this post